中央値

中央値（ちゅうおうち、英: median）あるいはメジアン、メディアンとは、データや集合の代表値の一つで、順位が中央である値のことである。ただし、データの大きさが偶数の場合は、中央順位2個の値の算術平均をとる。

例えば5人の年齢10歳、32歳、96歳、100歳、105歳からなるデータの中央値は、順位が上からも下からも3である96（歳）となる。0歳の子供が2人増えて7人になると、中央値は32歳となる。

平均値との関係

中央値は平均値と同様に集団の代表値を得る目的で使う。例えば年収からなるデータの場合を考えてみると分かりやすい。

一部の富裕層が平均年収をつり上げてしまう例を考える。人口100人の集落で、90人が年収200万円だとしても、10人が年収5000万円であれば平均年収は680万円となる。

一方中央値は、年収が低い順（高い順）に国民を並べたときにちょうど真ん中になる人の年収を表している。この場合、中央値はあいかわらず200万円であり、一部の富裕層の年収が中央値に与える影響はない。

例えば1人の億万長者が人口の少ない町に引っ越してくれば平均年収はつり上がってしまうが、年収の中央値はせいぜい1順位上がるに過ぎない。

厳密な定義

実確率変数 X の累積分布関数を F(x) とするとき、 F(x) は実数値非単調減少関数、右連続関数となる。この時、次の不等式を満たす実数 m を中央値（メディアン）と呼ぶ。

${\displaystyle \int _{-\infty }^{m}\mathrm {d} F(x)\geq {\frac {1}{2}}{\text{ and }}\int _{m}^{\infty }\mathrm {d} F(x)\geq {\frac {1}{2}}\,\!}$

ただし、積分記号はリーマン＝スティルチェス積分の意味である。

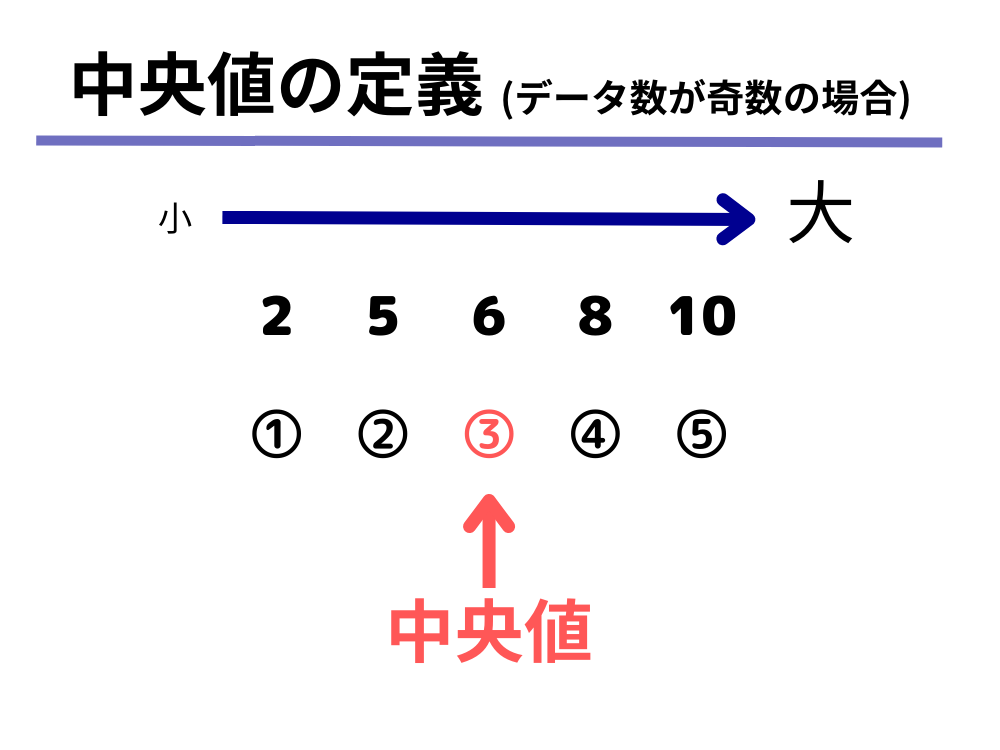
データの大きさが有限値（n とする）である場合は、以下のように簡単に記述することができる。（ただし、同一の順位が無いと仮定する。）

データの値を x₁, x₂, …, x_n とする。それらを小さい順に並べ替えたものを x′₁, x′₂, …, x′_n とするとき、${\displaystyle {\boldsymbol {x}}=(x_{1},x_{2},\cdots ,x_{n})}$ の中央値 ${\displaystyle \mathrm {Q} _{\frac {1}{2}}(x)}$ は

${\displaystyle \mathrm {Q} _{\frac {1}{2}}(x)={\begin{cases}x'_{\frac {n 1}{2}}&n{\text{ は 奇 数 }}\\{\dfrac {1}{2}}(x'_{\frac {n}{2}} x'_{{\frac {n}{2}} 1})&n{\text{ は 偶 数 }}\end{cases}}}$

により定義される。なお、単純に ${\displaystyle \mathrm {Q} _{\frac {1}{2}}(x)=x_{\frac {n}{2}}}$ とならないのは、${\displaystyle x}$ の添字が 0, …, n ではなく 1, …, n だからである。

中央値は平均絶対誤差 (mean absolute error, MAE)

${\displaystyle \operatorname {MAE} (t)={\frac {1}{n}}\sum _{i=1}^{n}|x_{i}-t|}$

を最小にする性質をもっている（ただし、そうなる値は一意ではない）。データの大きさが偶数のときは、その値 t は一意には定まらないが便宜上、上で述べた定義を採用する。

平均値との関係（数式的なもの）

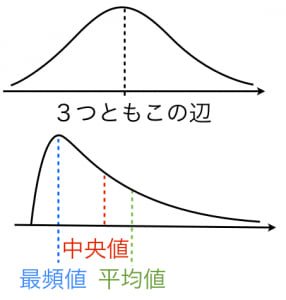
• 分布が対称であるデータに対しては、中央値は平均値に等しい。ただし、分布が対称でなくても、中央値と平均値が等しくなることもある。
• 以下の性質により、平均値よりも、全体の傾向を表す代表値として適切である場合が多い。
  • 平均値は、測定ミスなどによって発生する外れ値（他の値より著しく異なる値）に大きく影響され、誤差が大きくなったり、無意味な値となることがある。そのため、刈り込み、ロバスト統計などの対策が必要になる。しかし、中央値は外れ値にほとんど影響されないので、対策は不要である。
  • たとえばデータが正値のみといったように限定されている場合、そうでない場合と比べて分布はより非対称になりやすく、少数の大きな値に引きずられて平均値は大多数の分布より大きくずれることがある。しかし、中央値ではそういった影響はほとんどない。
  • ${\displaystyle \pm \infty }$ を含むデータに対しても中央値は有限となることがある。（平均値は、必ず無限または不定となる）
  • 分布の谷に位置するようなケースが、平均値に比べて少ない。（平均値は、2峰分布に対ししばしば谷に位置する）
• 中央値を求めるには、線形汎用選択アルゴリズムを使うと${\displaystyle \mathrm {O} (n)}$ の計算量で求められる（平均値も ${\displaystyle \mathrm {O} (n)}$）。逐次データが得られる場合は全てのデータを保持しておく必要があり、${\displaystyle \mathrm {O} (n)}$ のメモリを要する（平均値は ${\displaystyle \mathrm {O} (1)}$）。
• 代表値として平均値を使うときは、分布の広がりは分散または標準偏差で表すことが多い。それに対し、代表値として中央値を使うときは、分布の広がりは第3四分位点と第1四分位点の差である四分位範囲（英: interquartile range, IQR）で表すことが多い。

その他の性質

• 誤差はデータの誤差と同程度である。（平均値の誤差はデータの誤差の ${\displaystyle {\frac {1}{\sqrt {n}}}}$ 倍である）
• 中央値は、第2四分位数、50パーセンタイル、0.5クォンタイルでもある。

確率分布の中央値

1次元の確率分布 f(x) に対し、

${\displaystyle \int _{-\infty }^{m}f(x)\,\mathrm {d} x\geq {\frac {1}{2}}\;\mathrm {and} \;\int _{m}^{\infty }f(x)\,\mathrm {d} x\geq {\frac {1}{2}}}$

を満たす m を、中央値と呼ぶ。

関連項目

• 要約統計量
• 箱ひげ図
• 順序統計量
• ホッジス・レーマン推定量
• 幾何学的中央値

外部リンク

• 『中央値』 - コトバンク